 |
Un conjunto es una colección bien definida de objetos, que se denominan elementos o miembros del conjunto. Algunos sinónimos de “conjunto” son “clase”, “colección” y “familia”.
SEYMOUR LIPSCHUTZ Y MARC LIPSON
|
Definiciones
Las letras mayúsculas A, B, X, Y, . . . , denotan conjuntos y las minúsculas a, b, x, y, . . . , denotan elementos de conjuntos.
Pertenencia a un conjunto
- a ∈ S denota que a pertenece al conjunto S.
- a, b ∈ S denota que a y b pertenecen al conjunto S.
- Aquí ∈ es el símbolo para indicar “es un elementos de” y ∉ significa “no es un elemento de”.
Especificación de conjuntos
Una forma, de ser posible, consiste en enumerar sus elementos separados por comas y escritos entre llaves { }. La segunda es escribir las propiedades que caracterizan a los elementos del conjunto. La recta vertical | se lee “tal que” y la coma “y”.
Ejemplos:
- A = {2, 4, 6, 8} ó A = {x|x es entero par, x < 10}
- A = {2, 4, 6, 8, …} ó A = {x|x es entero par, x > 0}
- Sean E = {x | x2 − 3x + 2 = 0}, F = {2, 1} y G = {1, 2, 2, 1}, Entonces E = F = G.
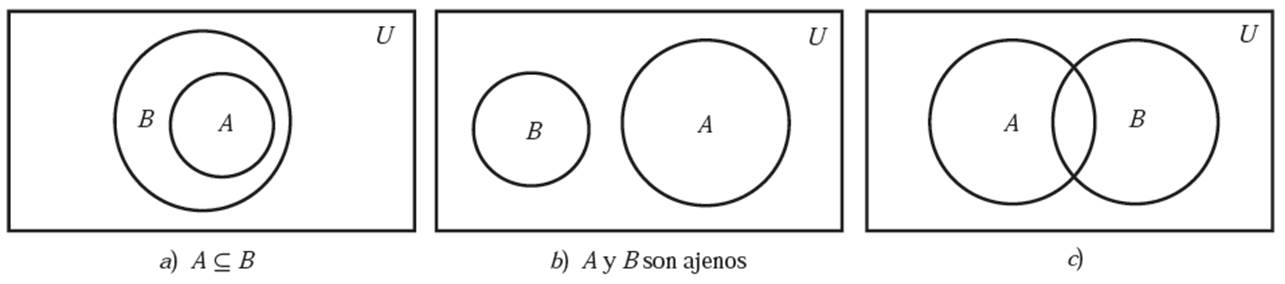
Subconjuntos
Suponga que todo elemento de un conjunto A también es un elemento de un conjunto B; es decir, si a ∈ A implica que a ∈ B. Entonces se dice que A es un subconjunto de B. También se dice que A está contenido en B o que B contiene a A.
Esta relación se escribe A ⊆ B o B ⊇ A
Dos conjuntos son iguales si ambos tienen los mismos elementos o, quivalentemente, si cada uno está contenido en el otro.
Es decir: A = B si y sólo si A ⊆ B y B ⊆ A
- Si A no es un subconjunto de B —porque al menos un elemento de A no pertenece a B— se escribe A ⊄ B
- Si A ⊆ B y A ≠ B, entonces se dice que A es un subconjunto propio de B
- Dos conjuntos A y B son ajenos o disjuntos, si no tienen elementos en común
Teoremas
Teorema 1: Sean A, B y C tres conjuntos cualesquiera. Entonces:
i) A ⊆ A
ii) Si A ⊆ B y B ⊆ A, entonces A = B
iii) Si A ⊆ B y B ⊆ C, entonces A ⊆ C
Teorema 2: Para cualquier conjunto A, se tiene Ø ⊆ A ⊆ U, Siendo U el conjunto universo y Ø el conjunto vacío.
Ejercicios:
- Considere los conjuntos: A = {1, 3, 4, 5, 7, 8, 9}, B = {1,3,4, 5, 9}, C = {1, 3}, D={4,5,9}
- ¿Qué propiedades se aplican entre ellos? Ø ⊆ A, … B ⊆ A, C ⊆ A, … C y D son propios, …
- Visualice gráficamente los teoremas de subconjuntos con diagramas de Venn
Diagramas de Venn
Un diagrama de Venn es un gráfico donde los conjuntos se representan con regiones encerradas en un plano. Aquí el conjunto universo U es el interior de un rectángulo y los otros conjuntos se representan por círculos dentro del rectángulo.
Operaciones con Conjuntos
Unión e Intersección
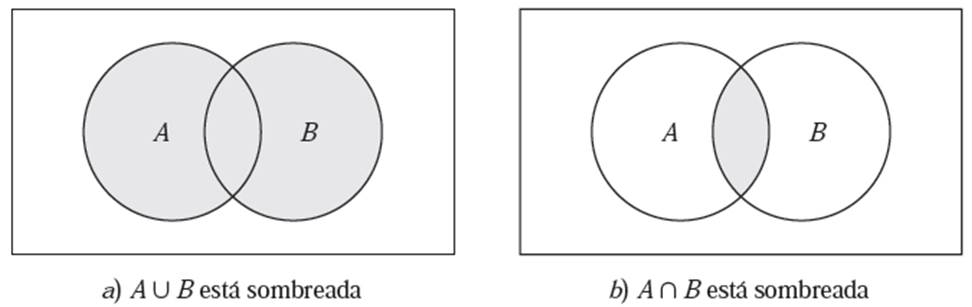
La unión de dos conjuntos A y B, que se denota por A ∪ B, es el conjunto de todos los elementos que pertenecen a A o a B; es decir,
A ∪ B = {x | x ∈ A o x ∈ B}
Expresión Lógica: p ∨ q siendo p: x ∈ A, q: x ∈ B
La intersección de dos conjuntos A y B, que se denota por A ∩ B , es el conjunto de los elementos que pertenecen tanto a A como a B; es decir,
A ∩ B = {x | x ∈ A y x ∈ B}
Expresión Lógica: p ∧ q siendo p: x ∈ A, q: x ∈ B
Teoremas
Teorema 3: Para dos conjuntos A y B arbitrarios, se tiene:
i) A ∩ B ⊆ A ⊆ A ∪ B y
ii) A ∩ B ⊆ B ⊆ A ∪ B
Teorema 4: Las siguientes expresiones son equivalentes:
A ⊆ B, A ∩ B = A, A ∪ B = B
Ejercicios:
- Visualice gráficamente los teoremas de subconjuntos con diagramas de Venn
- De los conjuntos L={3,5,7}, M={1,3,5,7,9}, N={5,7}, identifique casos en lo que se aplique los teoremas
Complementos, Diferencias y Diferencias Simétricas
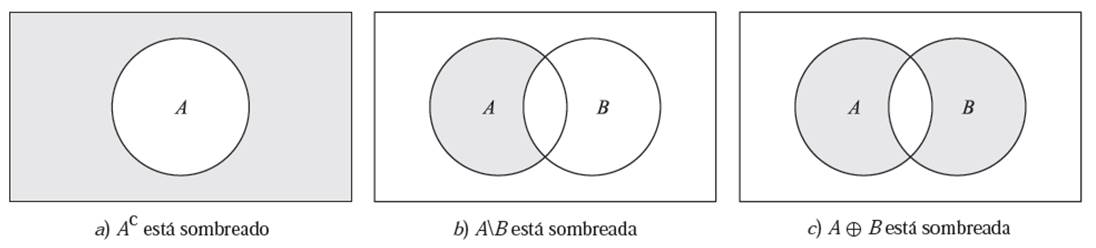
El complemento absoluto o, simplemente, el complemento de un conjunto A, denotado por Ac, es el conjunto de elementos que pertenecen a U, pero que no pertenecen a A. También se escribe A’ o Ᾱ. Es decir,
Ac = {x | x ∈ U, x ∉ A}
Expresión Lógica: p ∧ ¬ q siendo p: x ∈ U, q: x ∈ A
La diferencia de A y B, denotada por AB, es el conjunto de elementos que pertenecen a A pero que no pertenecen a B. También se escribe A – B. Es decir,
A-B = {x | x ∈ A, x ∉ B}
Expresión Lógica: p ∧ ¬ q siendo p: x ∈ A, q: x ∈ B
La diferencia simétrica de los conjuntos A y B, denotada por A ⊕ B, consta de los elementos que pertenecen a A o a B pero no a ambos. Es decir,
A ⊕ B = (A ∪ B)-(A ∩ B)
Expresión Lógica: (p ∨ q) ∧ ¬(p ∧ q) siendo p: x ∈ A, q: x ∈ B
o
A ⊕ B = (A-B) ∪ (B-A)
Expresión Lógica: (p ∧ ¬ q) ∨ (q ∧ ¬ p) siendo p: x ∈ A, q: x ∈ B
Ejemplos:
Suponga que U = N = {1, 2, 3, . . .} es el conjunto universo.
Sean A = {1, 2, 3, 4}, B = {3, 4, 5, 6, 7}, C = {2, 3, 8, 9,}, E = {2, 4, 6, . . .}
Entonces:
Ac = {5, 6, 7, . . .}, Bc = {1, 2, 8, 9, 10, . . .}, Ec = {1, 3, 5, 7, . . .}
También:
A-B = {1, 2}, AC = {1, 4}, B-C = {4, 5, 6, 7}, A-E = {1, 3},
B-A = {5, 6, 7}, CA = {8, 9}, C-B = {2, 8, 9}, E-A = {6, 8, 10, 12, . . .}.
Además:
A ⊕ B = (A-B) ∪ (B-A) = {1, 2, 5, 6, 7}, B⊕ C = {2, 4, 5, 6, 7, 8, 9},
A ⊕ C = (A-C) ∪ (B-C) = {1, 4, 8, 9}, A⊕ E = {1, 3, 6, 8, 10, . . .}
Ejemplo de Operaciones con Conjuntos a partir de las Proposiciones Lógicas:
Dados los conjuntos: U = {1, 2, 3, …, 8, 9} A = {1, 2, 3, 4} B = {2, 4, 6, 8} C = {3, 4, 5, 6}:
- Halle los conjuntos resultantes
- Represente cada caso con diagramas de Venn
- Formule cada caso en lenguaje proposicional y verifique cada caso con las tablas de verdad.
- Identifique casos de equivalencias lógicas y verifíquelas.
A ∩ (B ∪ C)
Sea p: x ∈ A q: x ∈ B r: x ∈ C
Expresión lógica: p ∧ (q ∨ r)
Verificación sobre la tabla de verdad de los x que cumplen con la proposición
p
|
q |
r |
p |
∧ |
(q |
∨ |
r) |
Valores |
| V |
V |
V |
|
V |
|
V |
|
4 |
| V |
V |
F |
|
V |
|
V |
|
2 |
| V |
F |
V |
|
V |
|
V |
|
3 |
| V |
F |
F |
|
F |
|
F |
|
|
| F |
V |
V |
|
F |
|
V |
|
|
| F |
V |
F |
|
F |
|
V |
|
|
| F |
F |
V |
|
F |
|
V |
|
|
| F |
F |
F |
|
F |
|
F |
|
|
| 1 |
1 |
1 |
1 |
3 |
1 |
2 |
1 |
|
Con lo que A ∩ (B ∪ C) = {2, 3, 4]
Álgebra de Conjuntos

Principio de Dualidad: Suponga que E es una ecuación de álgebra de conjuntos. El dual E* de E es la ecuación que se obtiene al sustituir cada aparición de ∪, ∩, U y Ø en E por ∩, ∪, Ø y U, respectivamente.
Regresar