|
|
Ejercicios Propuestos
Relaciones
Material de Estudio
- Seymour Lipschutz y Marc Lars Lipson. Matemáticas Discretas, tercera edición. Mc Graw Hill, México 2009. Estudio secciones 2.1 a 2.10 páginas 23-33. Problemas resueltos páginas 34-39, suplementarios páginas 40-42
- Richard Johnsonbaugh. Matemáticas Discretas, sexta edición. Pearson Educación. México 2005. Estudio secciones 3.1-3.3. Contenido y ejercicios páginas 116-137. Autoevaluación secciones 3.1-3.3 páginas 142-144.
Ejercicios Propuestos
1. Definiciones de relación: Resuelva
- 1.1) Dados los conjuntos C = {1, –3} y D = {2, 3, 6}, encontrar todos los pares ordenados (x, y) que satisfagan la relación R = {(x, y) | x + y = 3}, encontrar dominio y rango de la relación.
- 1.2) Sea A = {1, 2, 3, 4} y B = {4, 5, 6, 7, 8} y R la relación definida de A en B determinada por la regla “y es el doble de x” o “y = 2x”, encontrar todos los pares ordenados, dominio y rango de la relación.
- 1.3) Sea S la relación sobre el conjunto N de lo enteros positivos definida por la ecuación x + 3y = 13, esto es, S = {(x, y) | x + 3y = 13}, encontrar todos los pares ordenados, dominio y rango de la relación.
- 1.4) Sea R la relación de A = {1, 2, 3, 4} en B = {x, y, z} definida como R = {(1, y), (1, z), (3, y), (4, x), (4, z)}. Determine el dominio y el rango de R, y halle la relación inversa R-1 de R.
2. Represente gráficamente:
- 2.1) Represente gráficamente las relaciones resultantes de los ejercicios 1.1 al 1.4. Utilice para cada caso diagramas sagitales, matrices, grafos dirigidos y productos cartesianos.
- 2.2) Dibuje el grafo dirigido de la relación T sobre X = {1, 2, 3, 4} de finida por T = {(1, 1), (2, 2), (2, 3), (3, 2), (4, 2), (4, 4)}. Halle la Matriz M que representa la relación T.
- 2.3) Sea A = {1, 2, 3, 4, 6} y sea R la relación sobre A definida por “x divide a y”. Halle la relación R, dibuje el grafo dirigido y halle la matriz. (Los divisores de un número natural son los números naturales que lo pueden dividir, resultando de cociente otro número natural y de resto 0).
3. Composición entre relaciones
- 3.1) Sean A = {1, 2, 3}, B = {a, b, c) y C = {x, y, z}. Considere las siguientes relaciones R y S de A a B y de B a C, respectivamente, R = {(1, b), (2, a), (2, c)} y S = {(a, y), (b, x), (c, y), (c, z)}. Encuentre la relación composición R ◦ S gráficamente y por multiplicación de matrices.
4. Tipos de relaciones
- 4.1) En cada uno de los siguientes incisos se define una relación sobre los enteros positivos N:
-
“x es mayor que y”.- “xy es el cuadrado de un entero”.
- x + y = 10.
- x + 4y = 10.
Determine cuáles de esas relaciones son: a) reflexivas; b) simétricas; c) antisimétricas; d ) transitivas.
- 4.2) Proporcione un ejemplo de una relación R sobre A = {1, 2, 3} tal que:
-
R sea tanto simétrica como antisimétrica.- R no sea simétrica ni antisimétrica.
- 4.3) Sea R la relación sobre N de los enteros positivos definida por R = {(a, b)| a + b es par}, Es R una relación de equivalencia?
- 4.4) Sea R = {(1, 1), (1, 3), (3, 1), (3, 3). Es R una de equivalencia sobre A = {1, 2, 3}? Y sobre B = {1, 3}?
- 4.5) Construya un ejemplo de relaciones de orden parcial.
5. Sean R y S relaciones sobre un conjunto A. Suponga que A tiene tres elementos y mencione si cada una de las siguientes declaraciones es falsa o verdadera. Si es falsa, proporcione un contraejemplo sobre el conjunto: A = {1, 2, 3}:
- 5.1) Si R y S son simétricas, entonces R ∩ S es simétrica.
- 5.2) Si R y S son simétricas, entonces R ∪ S es simétrica.
- 5.3) Si R y S son reflexivas, entonces R ∩ S es reflexiva.
- 5.4) Si R y S son reflexivas, entonces R ∪ S es reflexiva.
- 5.5) Si R y S son transitivas, entonces R ∪ S es transitiva.
- 5.6) Si R y S son antisimétricas, entonces R ∪ S es antisimétrica.
- 5.7) Si R es antisimétrica, entonces R-1 es antisimétrica.
- 5.8) Si R es reflexiva, entonces R ∩ R-1 no es vacía.
- 5.9) Si R es simétrica, entonces R ∩ R-1 no es vacía.
Funciones
Material de Estudio
- Seymour Lipschutz y Marc Lars Lipson. Matemáticas Discretas, tercera edición. Mc Graw Hill, México 2009. Estudio secciones xx a xx páginas xx. Problemas resueltos páginas xx, suplementarios páginas xx
- Richard Johnsonbaugh. Matemáticas Discretas, sexta edición. Pearson Educación. México 2005. Estudio secciones xx. Contenido y ejercicios páginas xx. Autoevaluación secciones xx páginas xx.
Ejercicios propuestos
1. Considere las relaciones siguientes sobre el conjunto A = {1, 2, 3}:
f = {(1, 3), (2, 3), (3, 1)}, g= {(1, 2), (3, 1)}, h= {(1, 3), (2, 1), (1, 2), (3, 1)}, cuáles son o no funciones, explique la respuesta.
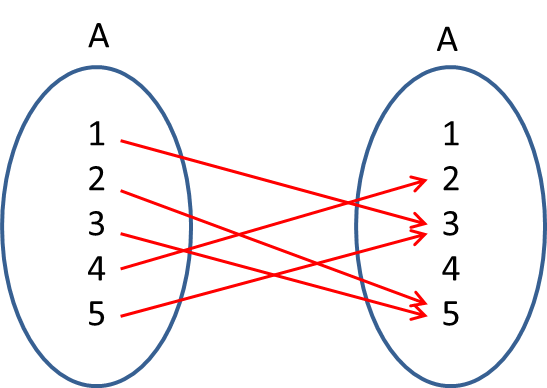
2. Considere el conjunto A = {1, 2, 3, 4, 5} y la función f: A → A definidos en la figura. Encuentre:
- La imagen de cada elemento de A
- La imagen f(A) de la función f.
3. Dada la función f(x) = x2, encuentre:
- El valor de la función para 5, -4 y 0.
- f(y+2)
- f (x+h) d)[f(x+h)-f(x)]/h]
4. Sea V = {1, 2, 3, 4}. Para las siguientes funciones f : V→V y g: V→V; encuentre:
- f ◦ g
- g ◦ f
- f ◦ f
Para f = {(1, 3), (2, 1), (3, 4), (4, 3)} y g = {(1, 2), (2, 3), (3, 1), (4, 1)}
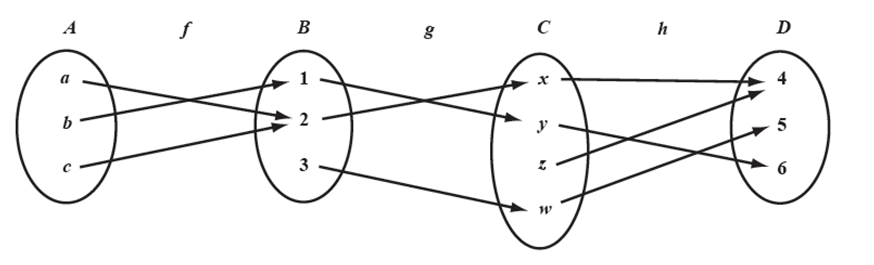
5. Sean las funciones f : A→B, g: B→C, h: C→D definidas en la figura, encuentre la composición de funciones h ◦ g ◦ f. Verifique los resultados de los ejercicios 4 y 5 utilizando el método de multiplicación de matrices
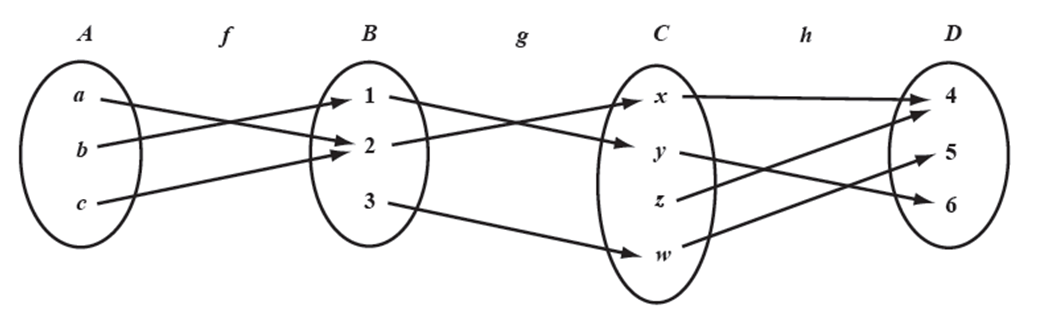
6. Sean las funciones f : A→B, g: B→C, h: C→D definidas por la figura. Determine si cada función es: a) sobre, b) uno a uno, c) invertible.
7. Sean las funciones f, g, h de V = {1, 2, 3, 4} en V definidas por:
f (n) = 6 − n, g(n) = 3, h = {(1, 2), (2, 3), (3, 4), (4, 1)}. Defina cuáles funciones son:
a) uno a uno; b) sobre; c) ambas; d ) ni uno a uno ni sobre.
Algoritmos
- Relación Reflexiva si/no porqué
- Relación Simétrica si/no porqué
- Relación Antisimétrica si/no porqué
- Transitiva vectores/matrices si/no porqué
- Transitiva por composición de relaciones si/no porqué
- Composición entre relaciones (para 2 o 3 relaciones)
- Evaluar un conjunto de pares ordenador y definir si es o no función, porqué
- Composición entre funciones (para 2 o 3 funciones)
- Inyectiva si/no porqué
- Sobreyectiva si/no porqué
- Biyectiva si/no porqué
Para la siguientes funciones matemáticas se debe generar los pares ordenados asociados a cada función. además de los resultados
Ejercicio 1.
Encuentre: a) 25 (mód 7); b) 25 (mód 5); c) −35 (mód 11); d ) −3 (mód 8).
Ejercicio 2.
Haga una Miscelánea de operaciones con aplicaciones de potencias y radicales en NetBeans.
Ejercicio 3.
- Evalúe: a) log2 8; b) log2 64; c) log10 100; d ) log10 0.001.
- Evalúe: a) log2 16; b) log3 27; c) log10 0.01.
Ejercicio 4.
Defina formalmente la sucesión 1, −1, 1, −1, . . . , desde n = 0 y n = 1.
Ejercicio 5.
5
∑ j(j + 1)/2
j=1
Ejercicio 6.
- Simplifique: a) n!/(n − 1)! ; b) (n + 2)!/n!.
- Encuentre: a) 3! + 4!; b) 3! (3! + 2!); c) 6!/5!; d ) 30!/28!
Ejercicio 7. Aplicación
Si A = {5, 7, 9} y B = {2, 4, 6, 8}, construya un proyecto NetBeans con una clase que cree objetos tipo par ordenado para manipularlos y obtener:
- Dados los pares ordenados de una relación de A en B, entregar los elementos del dominio y el codominio o rango.
- Encontrar todos los pares ordenados (x, y) que satisfagan la relación S = {(x, y) | x + 3y = 13}, encontrar dominio y rango de la relación.
- Cree un método que dada una relación, se identifique si es reflexiva, transitiva, simétrica y antisimétrica.
- Dada una relación de A en B, defiir si es una función.
- Dada una función f : A → B, identifique si es uno a uno, sobre o invertible.
- Creea métodos para generar los pares ordenados y el resultado (cuando sea el caso) de las funciones matemáticas.
|
|